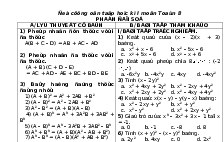Đề cương ôn tập chương 2 Hình học 8
Nội dung tài liệu
Tải xuống
Link tài liệu:
Các tài liệu liên quan
-
![Đề cương ôn thi học kì 1 Toán 8]()
-
![Đề cương ôn tập Toán 8 học kì 2]()
-
![Các chuyên đề ôn tập các dạng hình học toán 8]()
-
![Các chuyên đề ôn tập các dạng hình học toán 8]()
-
![Các chuyên đề ôn tập Đại số 8]()
-
![Tài liệu ôn thi HSG Toán 8 đại số]()
-
![Toán 8: Chuyên đề phân tích đa thức thành nhân tử]()
-
![Các chuyên đề ôn HSG Toán 8]()
-
![Các chuyên đề ôn toán hình lớp 8]()
-
![350 bài tập trắc nghiệm phép nhân và phép chia các đa thức]()